Így, hozzávetőlegesen javított kúpos technika alkalmazásával.
A $ \ Delta V $ pillanatnyi (pl. kémiai meghajtású) manővereket használva meghatározható ennek az egyenletnek az ismételt alkalmazásával, amely egyszerűen azt mondja, hogy az összes energia a kinetikus energia és a potenciális energia összege:
$ \ mathcal {E} = \ frac {v ^ 2} {2} - \ frac {\ mu} {r} $
ahol $ \ mathcal {E} $ az objektum egységnyi tömegére eső összes energiája vagy a "fajlagos energia", $ v $ az objektum sebessége az aktuális helyzetben, $ \ mu $ a GM a központi test, azaz Newton gravitációs állandója a tömegének a szorosa, és $ r $ az aktuális távolság a központi test közepétől.
A legfontosabb, hogy az objektum teljes energiája mozgás a pályán.
Azt a tényt is felhasználjuk, hogy a pályák ellipszisek, és ezt az egyenletet, amely meghatározza azt a mozgásállandót a pálya apszisaiból, vagyis a legközelebbi és legtávolabbi pontok sugarait a pálya, $ r_1 $ és $ r_2 $:
$ \ mathcal {E } = - {\ mu \ over r_1 + r_2} $
Menekülés vagy bejutás a menekülési pályáról:
$ \ mathcal {E} = {v_ \ infty ^ 2 \ több mint 2} $
ahol $ v_ \ infty $ a sebesség a végtelenséghez képest a testhez képest.
Ehhez a problémához a következőket definiáljuk:
$ \ mu_E $ = A Föld GM értéke.
$ \ mu_M $ = a Hold GM értéke.
$ r_E $ = alacsony Föld pálya sugara.
$ r_M $ = alacsony Hold pálya sugara.
$ a_M $ = a Hold féltengelye (átlagos sugara) a Föld körül kering.
Az egyszerűség kedvéért azt feltételezzük, hogy a Hold pályája kör alakú, ami nincs messze az igazságtól.
A fentiek felhasználásával alacsony földi pályán a $ v_ {LEO} $ keringési sebességgel rendelkezünk:
$ - {\ mu_E \ over 2r_E} = \ frac {v_E ^ 2} {2} - \ frac {\ mu_E} {r_E} $
amely a következőt adja:
$ v_ {LEO} = \ sqrt {\ mu_E \ over r_E} $
A Hohmann-transzfer a Földről a Holdra a Föld körüli elliptikus pálya fele periapszis $ r_E $ és apoapsis $ a_M $ értékkel. A $ v $ sebességhez az adott pálya bármely $ r $ sugaránál megvan:
$ - {\ mu_E \ r_E + a_M} = \ frac {v ^ 2} {2} - \ frac {\ mu_E} {r} $
Az átviteli pálya sebessége a az alacsony földi pálya sugara, vagyis annak periapisa:
$ v_p = \ sqrt {2a_M \ mu_E \ r_E \ bal felett (a_M + r_E \ jobb)} $
Az alacsony földi pálya elhagyási sebessége az átviteli pályára akkor:
$ \ Delta V_ {inject} = v_p-v_ {LEO} $
Ennyi el kell repülnie a Hold mellett, ez a kérdés címe. Bár a kérdőívben azt kérdezi, hogyan lehet alacsony holdi pályára jutni. Szüksége van egy újabb manőverre és további hajtóanyagra, hogy lelassuljon és bejusson egy pályára.
A LEO érdekében tett lépések alkalmazásával a hold alacsony pálya sebessége: $ v_ {LLO} $:
$ v_ {LLO} = \ sqrt {\ mu_M \ over r_M} $
Hasonlóképpen a Hold sebessége a Föld körüli pályáján:
$ v_M = \ sqrt {\ mu_E \ over a_M} $
Az átviteli pálya sebessége a Hold sugarán, azaz apoapszisában a következő:
$ v_a = \ sqrt {2r_E \ mu_E \ a_M \ bal felett (a_M + r_E \ jobb)} $
A sebesség a közeledő Holdhoz viszonyítva, ha a Hold nem volt ott:
$ v_ \ infty = v_M-v_a $
Ez megadja a sebességet a megközelítéskor, amikor a Hold ott van, a Hold bármely sugarához:
$ {v_ \ infty ^ 2 \ over 2} = \ frac {v ^ 2} {2} - \ frac {\ mu_M} {r} $
Egy alacsony holdi pálya sugaránál ez a sebesség :
$ v_L = \ sqrt {\ left (v_M-v_a \ right) ^ 2 + {2 \ mu_M \ over r_M}} $
A pályára történő beszálláshoz szükségünk van lassítani a Holdhoz képest:
$ \ Delta V_ {insert} = v_L-v_ {LLO} $
A teljes $ \ Delta V $ értéke majd:
$ \ Delta V_ {total} = v_p-v_ {LEO} + v_L-v_ {LLO} $
Csatlakoztassa a számokat, és feltételezzen 200 km LEO-t és 100-at km LLO magasságot kapunk:
$ \ Delta V_ {inject} = 3,13 \, \ mathrm {km \ over s} $
$ \ Delta V_ {insert} = 0,82 \, \ mathrm {km \ over s} $
$ \ Delta V_ {total} = 3,95 \, \ mathrm {km \ over s} $
Ez közel áll ahhoz a válaszhoz, amelyet a teljes integráció során kap, lehetővé téve, hogy a Hold gravitációja jóval azelőtt elkezdhesse húzni az űrhajót, mielőtt a Hold távolságába kerülne. Ez kissé megnöveli az űrhajó sebességét a Holdhoz viszonyítva, növelve a $ \ Delta V $ értéket, hogy egy kicsit beillesszen.
Ez egy közvetlen transzfer, amely napok alatt teljesíthető. Ha hajlandó néhány hónapot igénybe venni, vannak alacsonyabb $ \ Delta V $ utak, amelyek általánosított Lagrange-pontokon mennek keresztül. Megtakaríthat 0,1 USD nagyságrendű \, \ mathrm {km \ over s} $ nagyságrendet.
Mivel ez közösségi wiki, a a megfelelő linkről egy holdrepüléshez és visszatéréshez. A küldetés pályája a következő:
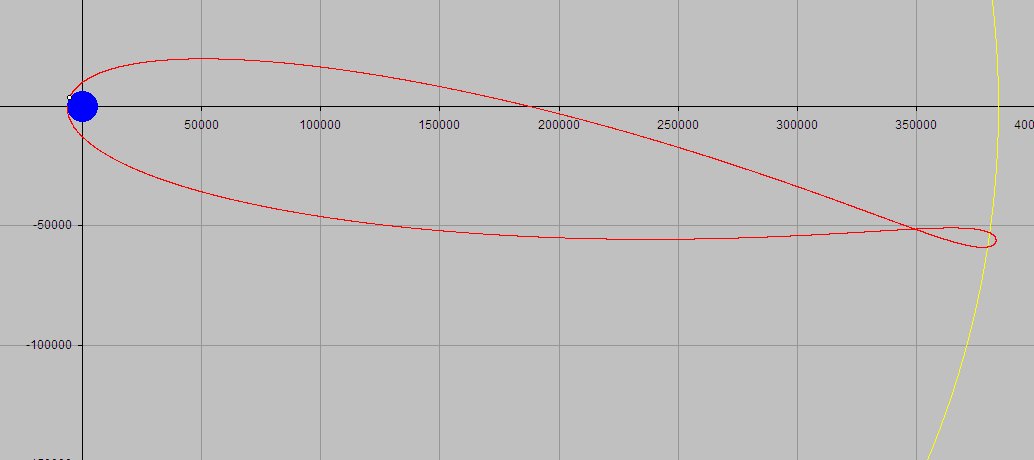
Ami a Delta v értéket illeti:
A TLI előtt az űrhajó alacsonyan van kör alakú parkoló kering a Föld körül. Ebben a példában feltételeztük, hogy a parkolási pálya magassága 185 kilométer, a TLI delta-v pedig 3150 m / s .
Ne feledje, hogy ez egy bizonyos holdmagasság társítva hozzá.
A pericintion az űrszonda pályájának a Holdhoz legközelebb eső pontja. A szabad visszatérési pálya esetében a pericintion magassága általában 100–1 500 tengeri mérföld (185–2 800 km) - lásd az ábrát. A pericintion magassága ebben a példában 1 446 kilométer.
Ha legelni akarta a Hold felszínét, akkor módosítania kell a paramétereket. Szerencsére van elég erre. A vezérelhető változók a következők:
- az a sebesség, amelyet a leégés során nyer a LEO-ban
- az időzítés, amelyen ezt végrehajtja.
Ez azt feltételezi, hogy minden 2D-s síkban van, mint a fenti képen. A küldetés elvégzéséhez (és a halál elkerülése érdekében) irányítania kell a következőket:
- a minimális magasság a Hold felett
- a Föld becsapódási helye
Ezeket azért sorolom fel, mert a vezérelhető változók száma megegyezik a vezérelni kívánt változók számával. Ez azt bizonyítja, hogy bármely adott repülési távolság elérhető, de azt is bizonyítja, hogy ennek eléréséhez módosítania kell az égési időt. Tehát ahhoz, hogy közelebbről megközelíthesse a holdat, meg kell változtatnia a hajtóanyag követelményét. Hogy ezzel többé-kevésbé sikerül-e, nem tudom.